Skip to main content Link Menu Expand (external link) Document Search Copy Copied
PP-f24

Programming Assignment IV: MPI Programming

Parallel Programming by Prof. Yi-Ping You

Due date: 23:59, November 21, Thursday, 2024

The purpose of this assignment is to familiarize yourself with MPI programming.

Table of contents

  1. Programming Assignment IV: MPI Programming
    1. 0. Using Workstation
    2. 1. Part 1: Getting Familiar with MPI Programming
      1. 1.1 MPI Hello World, Getting Familiar with the MPI Environment
      2. 1.2 Calculating PI with MPI
        1. 1.2.1 MPI Blocking Communication & Linear Reduction Algorithm
        2. 1.2.2 MPI Blocking Communication & Binary Tree Reduction Communication Algorithm
        3. 1.2.3 MPI Non-Blocking Communication & Linear Reduction Algorithm
        4. 1.2.4 MPI Collective: MPI_Gather
        5. 1.2.5 MPI Collective: MPI_Reduce
        6. 1.2.6 MPI Windows and One-Sided Communication & Linear Reduction Algorithm
    3. 2. Part 2: Matrix Multiplication with MPI
    4. 3. Requirements
      1. 3.1 Requirements for Part One
      2. 3.2 Requirements for Part Two
    5. 4. Grading Policy
    6. 5. Evaluation Platform
    7. 6. Submission
    8. 7. References

We provide dedicated workstations for this course, you can access the workstations by ssh or use your own environment to complete the assignment.

HostnameIPPortUser Name
hpc1.cs.nycu.edu.tw140.113.215.19810001-10005{student_id}

Login example:

ssh <student_id>@hpc1.cs.nycu.edu.tw -p <port>

Get the source code:

wget https://nycu-sslab.github.io/PP-f24/assignments/HW4/HW4.zip
unzip HW4.zip -d HW4
cd HW4

0. Using Workstation

In this assignment, you’ll need to use srun --mpi=pmix to run MPI programs on our workstation. Unlike previous assignments where physical threads were allocated with srun -c, here you’ll need to specify the number of nodes on which to run your program.

Here is an example of how to run an MPI program on 4 dedicated nodes:

srun --mpi=pmix -N 4 mpi_hello

By default, each node will run 1 process. You can use the -n option to specify how many processes should be running this MPI program:

srun --mpi=pmix -N 2 -n 4 mpi_hello

The command above will run 4 processes on 2 dedicated nodes. You can experiment with different settings, but for this assignment, we only run 1 process on each of the dedicated node.

1. Part 1: Getting Familiar with MPI Programming

1.1 MPI Hello World, Getting Familiar with the MPI Environment

Here we’re going to implement our first MPI program.

Expected knowledge includes basic understanding of the MPI environment, how to compile an MPI program, how to set the number of MPI processes, and retrieve the rank of the process and number of MPI processes at runtime.

There is a starter code for you. Look at hello.cc. Please finish the _TODO_s with the MPI_Comm_size and MPI_Comm_rank functions.

We will work on NFS (which is already set up ), so we don’t need to copy and compile the code again and again on different nodes.

Let’s first compile hello.cc on NFS:

mpicxx hello.cc -o mpi_hello

Use srun to start MPI processes:

srun --mpi=pmix -N 8 mpi_hello

This command will launch eight processes to run mpi_hello on eight nodes (each node run one process), and you should be able to get an output similar to:

Hello world from processor hpc054, rank 1 out of 8 processors
Hello world from processor hpc053, rank 0 out of 8 processors
Hello world from processor hpc055, rank 2 out of 8 processors
Hello world from processor hpc063, rank 5 out of 8 processors
Hello world from processor hpc064, rank 6 out of 8 processors
Hello world from processor hpc062, rank 4 out of 8 processors
Hello world from processor hpc065, rank 7 out of 8 processors
Hello world from processor hpc061, rank 3 out of 8 processors

Code Implementation: (8 points)

  • Complete hello.cc: the Hello World code in C.
  • srun --mpi=pmix -N 8 mpi_hello should run correctly
  • The argument of -N is expected to be any positive integer less than or equal to 16.

1.2 Calculating PI with MPI

In this exercise, we are going to parallelize the calculation of Pi following a Monte Carlo method and using different communication functions and measure their performance.

Expected knowledge is MPI blocking and non-blocking communication, collective operations, and one-sided communication.

Instructions: Write different versions of MPI codes to calculate Pi. The technique we are implementing relies on random sampling to obtain numerical results. You have already implemented this in the previous assignments.

1.2.1 MPI Blocking Communication & Linear Reduction Algorithm

In our parallel implementation, we split the number of iterations of the main loop into all the processes (i.e., NUM_ITER / num_ranks). Each process will calculate an intermediate count, which is going to be used afterward to calculate the final value of Pi.

To calculate Pi, you need to send all the intermediate counts of each process to rank 0. This communication algorithm for reduction operation is called linear as the communication costs scales as the number of processes.

An example of linear reduction with eight processes is as follows:

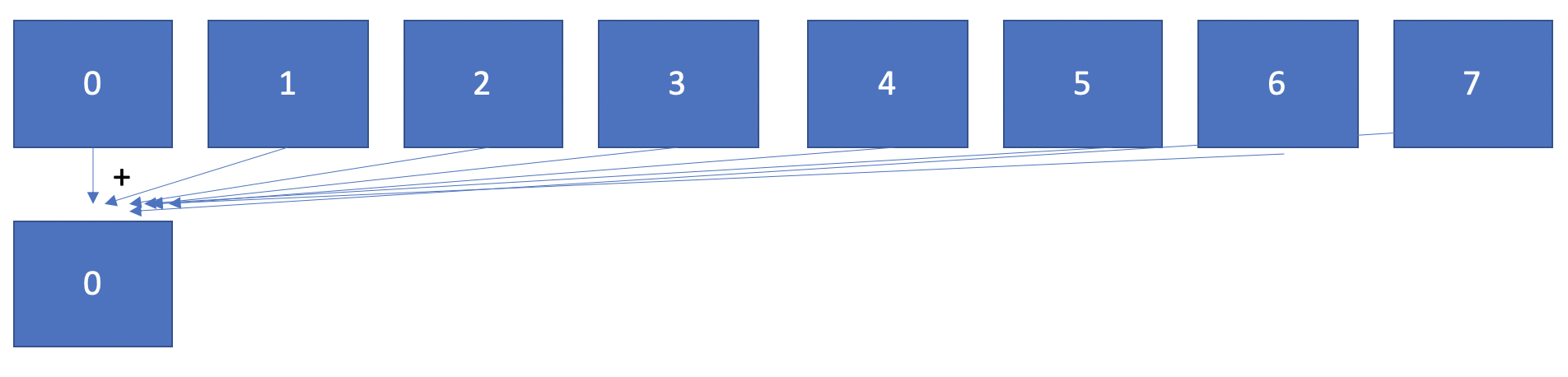
image

Rank 0 is going to receive the intermediate count calculated by each process and accumulate them to its own count value. (Rank 0 also needs to calculate a count, and this stands for the following sections in Part One.) Finally, after rank 0 has received and accumulated all the intermediate counts, it will calculate Pi and show the result, as in the original code.

Implement this code using blocking communication and test its performance.

Hint 1. Change the main loop to include the number of iterations per process, and not NUM_ITER (which is the total number of iterations).

Hint 2. Do not forget to multiply the seed of srand() with the rank of each process (e.g., “rank * SEED”) to ensure the RNGs of processes generate different random numbers.

There is a starter code pi_block_linear.cc for you.

mpicxx pi_block_linear.cc -o pi_block_linear; srun --mpi=pmix -N 4 pi_block_linear 1000000000

Code Implementation: (12 points)

  • Complete pi_block_linear.cc: the MPI block communication for PI.
  • Implement the code using a linear algorithm with MPI_Send/MPI_Recv.
  • Do not modify the output messages.
  • mpicxx pi_block_linear.cc -o pi_block_linear; srun --mpi=pmix -N 4 pi_block_linear 1000000000 should run correctly.
  • The argument of -N is expected to be any positive integer less than or equal to 16.
  • srun --mpi=pmix -N 4 pi_block_linear 1000000000 should not be more than 15% slower than the TA’s reference time.

1.2.2 MPI Blocking Communication & Binary Tree Reduction Communication Algorithm

Implement the binary tree communication algorithm for performing the reduction on rank 0 using blocking communication (e.g., MPI_Send/MPI_Recv).

The communication pattern for a reduction with a binary tree with eight processes is as follows:

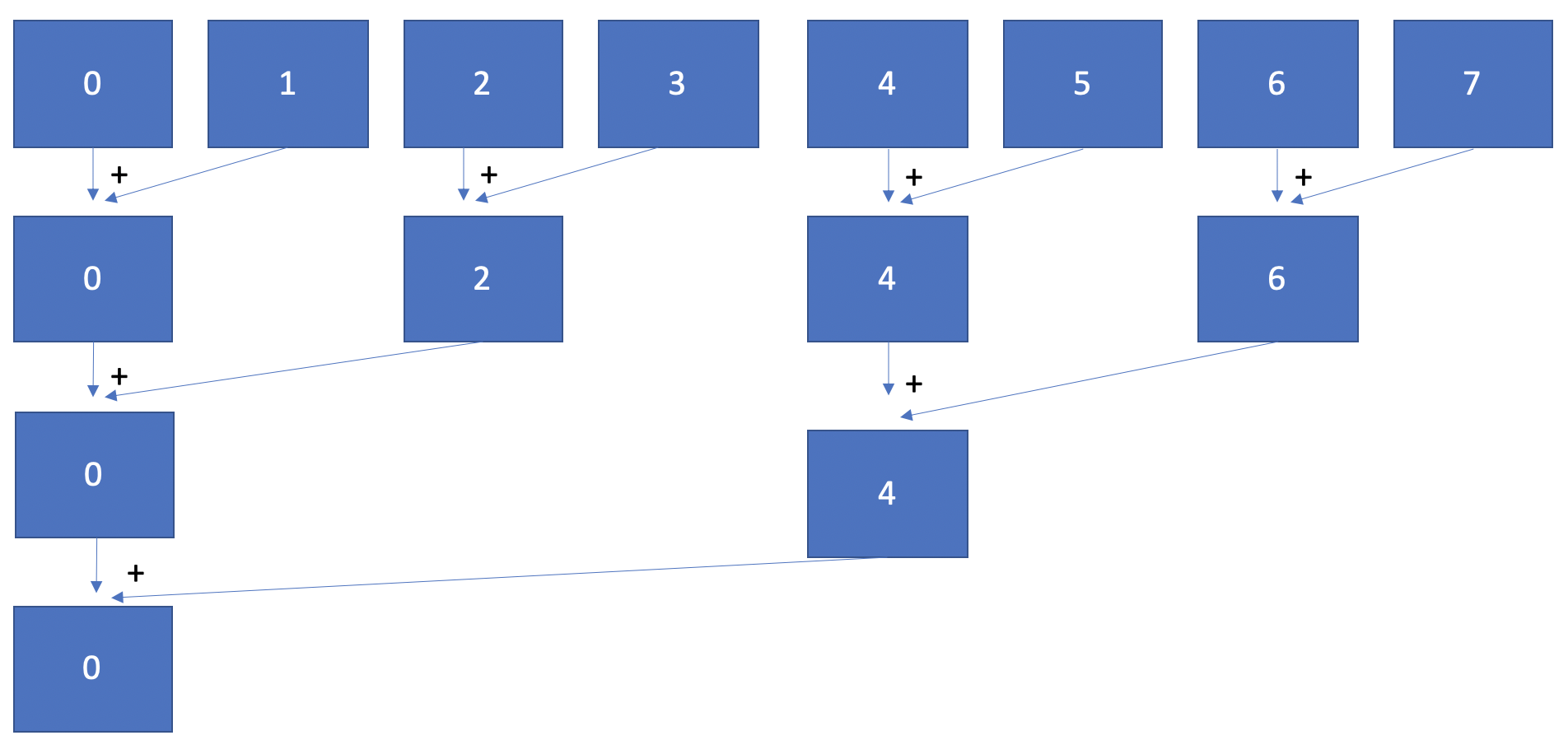
image

In you implementation, you can assume that we use a power-of-two number of processes.

There is a starter code pi_block_tree.cc for you.

mpicxx pi_block_tree.cc -o pi_block_tree; srun --mpi=pmix -N 4 pi_block_tree 1000000000

Code Implementation: (12 points)

  • Complete pi_block_tree.cc: the MPI block communication for PI.
  • Implement the code using a binary tree reduction algorithm with MPI_Send/MPI_Recv.
  • Do not modify the output messages.
  • mpicxx pi_block_tree.cc -o pi_block_tree; srun --mpi=pmix -N 4 pi_block_tree 1000000000 should run correctly.
  • The argument of -N is expected to be any power-of-two number less than or equal to 16.
  • srun --mpi=pmix -N 4 pi_block_tree 1000000000 should not be more than 15% slower than the TA’s reference time.

1.2.3 MPI Non-Blocking Communication & Linear Reduction Algorithm

Use non-blocking communication for the linear reduction operation (in Section 1.2.1).

Hint: Use a non-blocking MPI_Irecv() (MPI Receive with Immediate return). The basic idea is that rank 0 is going to issue all the receive operations and then wait for them to finish. You can either use MPI_Wait() individually to wait for each request to finish or MPI_Waitall(). Regardless of your decision, keep in mind that we want you to perform the receive operations in parallel. Thus, do not call MPI_Irecv() and immediately MPI_Wait()! In addition, we recommend you allocate an array of MPI_Request and also an array of counts (i.e., one for each receive needed).

There is a starter code pi_nonblock_linear.cc for you.

mpicxx pi_nonblock_linear.cc -o pi_nonblock_linear; srun --mpi=pmix -N 4 pi_nonblock_linear 1000000000

Code Implementation: (12 points)

  • Complete pi_nonblock_linear.cc: the MPI non-blocking communication for PI.
  • Implement the code using a non-blocking algorithm with MPI_Send/MPI_IRecv/MPI_Wait/MPI_Waitall.
  • Do not modify the output messages.
  • mpicxx pi_nonblock_linear.cc -o pi_nonblock_linear; srun --mpi=pmix -N 4 pi_nonblock_linear 1000000000 should run correctly.
  • The argument of -N is expected to be any positive integer less than or equal to 16.
  • srun --mpi=pmix -N 4 pi_nonblock_linear 1000000000 should not be more than 15% slower than the TA’s reference time.

1.2.4 MPI Collective: MPI_Gather

Use the collective MPI_Gather() operation, instead of point-to-point communication.

Hint: You can keep rank 0 as the root of the communication and still make this process aggregate manually the intermediate counts. Remember that the goal of MPI_Gather() is to provide the root with an array of all the intermediate values. Reuse the array of counts as the output for the gather operation.

There is a starter code pi_gather.cc for you.

mpicxx pi_gather.cc -o pi_gather; srun --mpi=pmix -N 4 pi_gather 1000000000

Code Implementation: (12 points)

  • Complete pi_gather.cc: the MPI gather communication for PI.
  • Implement the code using MPI_Gather.
  • Do not modify the output messages.
  • mpicxx pi_gather.cc -o pi_gather; srun --mpi=pmix -N 4 pi_gather 1000000000 should run correctly.
  • The argument of -N is expected to be any positive integer less than or equal to 16.
  • srun --mpi=pmix -N 4 pi_gather 1000000000 should not be more than 15% slower than the TA’s reference time.

1.2.5 MPI Collective: MPI_Reduce

Use the collective MPI_Reduce() operation.

Hint 1: Remember that the goal of MPI_Reduce() is to perform a collective computation. Use the MPI_SUM operator to aggregate all the intermediate count values into rank 0, But, watch out: rank 0 has to provide its own count as well, alongside the one from the other processes.

Hint 2: The send buffer of MPI_Reduce() must not match the receive buffer. In other words, use a different variable on rank 0 to store the result.

There is a starter code pi_reduce.cc for you.

mpicxx pi_reduce.cc -o pi_reduce; srun --mpi=pmix -N 4 pi_reduce 1000000000

Code Implementation: (12 points)

  • Complete pi_reduce.cc: the MPI reduce communication for PI.
  • Implement the code using MPI_Reduce.
  • Do not modify the output messages.
  • mpicxx pi_reduce.cc -o pi_reduce; srun --mpi=pmix -N 4 pi_reduce 1000000000 should run correctly.
  • The argument of -N is expected to be any positive integer less than or equal to 16.
  • srun --mpi=pmix -N 4 pi_reduce 1000000000 should not be more than 15% slower than the TA’s reference time.

1.2.6 MPI Windows and One-Sided Communication & Linear Reduction Algorithm

Use MPI Windows and MPI one-sided communication, which we didn’t cover this in class. You can choose the functions you’d like to use but remember that there is a reduction on the same MPI window from many processes! You may refer to one_side_example.c to get familiar with it.

There is a starter code pi_one_side.cc for you.

mpicxx pi_one_side.cc -o pi_one_side; srun --mpi=pmix -N 4 pi_one_side 1000000000

Code Implementation: (12 points)

  • Complete pi_one_side.cc: the MPI one sided communication for PI.
  • Implement the code using MPI_Win_* (or MPI_Put, MPI_Get, and MPI_Accumulate). You only need to implement the first one, and the remainings are optional.
  • Do not modify the output messages.
  • mpicxx pi_one_side.cc -o pi_one_side; srun --mpi=pmix -N 4 pi_one_side 1000000000 should run correctly.
  • The argument of -N is expected to be any positive integer less than or equal to 16.
  • srun --mpi=pmix -N 4 pi_one_side 1000000000 should not be more than 15% slower than the TA’s reference time.

2. Part 2: Matrix Multiplication with MPI

Write a MPI program which takes an $n \times m$ matrix $A$ and an $m \times l$ matrix $B$, and stores their product in an $n \times l$ matrix $C$. An element of matrix $C$ is obtained by the following formula:

\[c_{ij} = \sum_{k=1}^m a_{ik}b_{kj}\]

where $a_{ij}$, $b_{ij}$ and $c_{ij}$ are elements of $A$, $B$, and $C$, respectively.

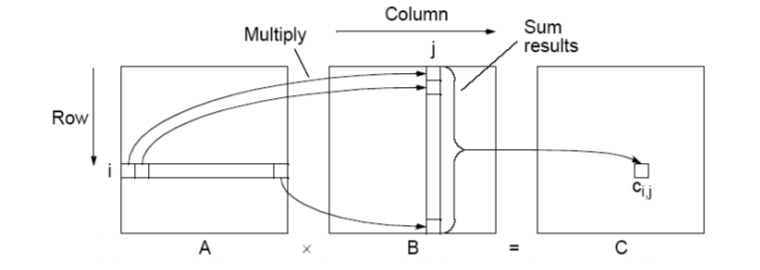
Matrix Figure

Your mission is to calculate the matrix multiplication as fast as possible. You may try many methods (Ex: tiling or some algorithms. Note that SIMD isn’t allowed here!) to achieve a higher performance. You are allowed to use any code on the Internet, but you need to re-write the code yourself, which means copying and pasting is not allowed. In addition, you are not allowed to use any third-party library; that is, you have to write your MPI program from scratch. Furthermore, each node is allowed to run a single-threaded process, so using OpenMP, Pthread, fork, GPU, etc. are not allowed.

If you are not sure about the rule, ask on our E3 forum!

Constraints

  1. $1 ≤ n, m, l ≤ 10000$
  2. $0 ≤ a_{ij}, b_{ij} ≤ 100$

Data Sets

There are two data sets. The table shows the credit, the range of $n$, $m$, and $l$, and the hosts used for each data set. You can find the data sets in /share/hwdata/HW4/testcase.

SetCreditn, m, l
110 points300-500
210 points1000-2000

You may have different implementations for the two data sets.

Notice that only one process per node is allowed.

3. Requirements

3.1 Requirements for Part One

  • Code implementation (following the instructions in Sections 1.2.1-1.2.6
    • hello.cc
    • pi_block_linear.cc
    • pi_block_tree.cc
    • pi_gather.cc
    • pi_nonblock_linear.cc
    • pi_reduce.cc
    • pi_one_side.cc

3.2 Requirements for Part Two

  • Code implementation
    • You should implement the functions in matmul.cc to calculate the matrix multiplication as described in Section 2.
    • Your program will be evaluated with command make; srun --mpi=pmix -N %N% matmul %data_file%, where N is 2-8, and data_file is the input.

4. Grading Policy

NO CHEATING!! You will receive no credit if you are found cheating.

Total of 100%:

  • part 1 (80%):
    • Implementation correctness and performance
  • part 2 (20%):
    • Performance: 20% (10% for each data set)
      • Evaluations will be conducted for each data set with the metric below.

Metric (for each data set):

\[\begin{cases} 40\%, \text{if} \; Y < R \times 2 \\\\ 20\%, \text{otherwise} \; \end{cases} + \begin{cases} \frac{T-Y}{T-R} \times 60\%, \text{if} \; Y < T \\\\ 0\%, \text{otherwise} \; \end{cases}\]

Where $Y$ and $R$ represent your program’s execution time and the reference time, respectively, and $T = R \times 1.5$.

All submissions receive a minimum of 20%. Programs no slower than 2x the reference time earn 40%. The remaining 60% is scaled based on runtime relative to the reference time.

5. Evaluation Platform

Your program should be able to run on UNIX-like OS platforms. We will evaluate your programs on the workstations dedicated for this course.

The workstations are based on Debian 12.6.0 with Intel(R) Core(TM) i5-10500 CPU @ 3.10GHz and Intel(R) Core(TM) i5-7500 CPU @ 3.40GHz processors and GeForce GTX 1060 6GB. g++-12, clang++-11, and CUDA 12.5.1 have been installed.

Please run the provided testing script test_hw4 before submitting your assignment.

Run test_hw4 in a directory that contains your HW4_XXXXXXX.zip file on the workstation. test_hw4 checks if the ZIP hierarchy is correct and runs graders to check your answer, although for reference only. For performance tuning with faster feedback, you can pass the -s (--skip-part1) option to skip the testing of Part 1.

test_hw4:

  • Check if the ZIP hierarchy is correct.
  • Part 1: Check the correctness and the performance.
  • Part 2: Evaluate the performance for the public data (in average time).

6. Submission

All your files should be organized in the following hierarchy and zipped into a .zip file, named HW4_xxxxxxx.zip, where xxxxxxx is your student ID.

Directory structure inside the zipped file:

  • HW4_xxxxxxx.zip (root)
    • part1
      • hello.cc
      • pi_block_linear.cc
      • pi_block_tree.cc
      • pi_gather.cc
      • pi_nonblock_linear.cc
      • pi_reduce.cc
      • pi_one_side.cc
    • part2
      • matmul.cc

Zip the file:

zip HW4_xxxxxxx.zip -r part1 part2

Be sure to upload your zipped file to new E3 e-Campus system by the due date.

You will get NO POINT if your ZIP’s name is wrong or the ZIP hierarchy is incorrect.

You will get a 5-point penalty if you hand out unnecessary files (e.g., obj files, .vscode, .__MACOSX).

7. References

Back to top

This website is built using Kevin Lin's Just the Class Jekyll template.